univariateML

R-CMD-check Codecov test coverage Project Status: Active – The project has reached a stable, usable state and is being actively developed. DOI CRAN_Status_Badge

Overview

univariateML is an R-package for user-friendly maximum likelihood estimation of a selection of parametric univariate densities and probability mass functions. In addition to basic estimation capabilities, this package support visualization through plot and qqmlplot, model selection by AIC and BIC, confidence sets through the parametric bootstrap with bootstrapml, and convenience functions such as the density, distribution function, quantile function, and random sampling at the estimated distribution parameters.

Installation

Use the following command from inside R to install from CRAN.

install.packages("univariateML")

Or install the development version from Github.

# install.packages("devtools")
devtools::install_github("JonasMoss/univariateML")

Usage

The core of univariateML are the ml*** functions, where *** is a distribution suffix such as norm, gamma, or weibull.

library("univariateML")
mlweibull(egypt$age)
#> Loading required package: intervals
#> Maximum likelihood estimates for the Weibull model 
#>  shape   scale  
#>  1.404  33.564

Now we can visually assess the fit of the Weibull model to the egypt data with a plot.

hist(egypt$age, freq = FALSE, xlab = "Mortality", main = "Egypt")
lines(mlweibull(egypt$age))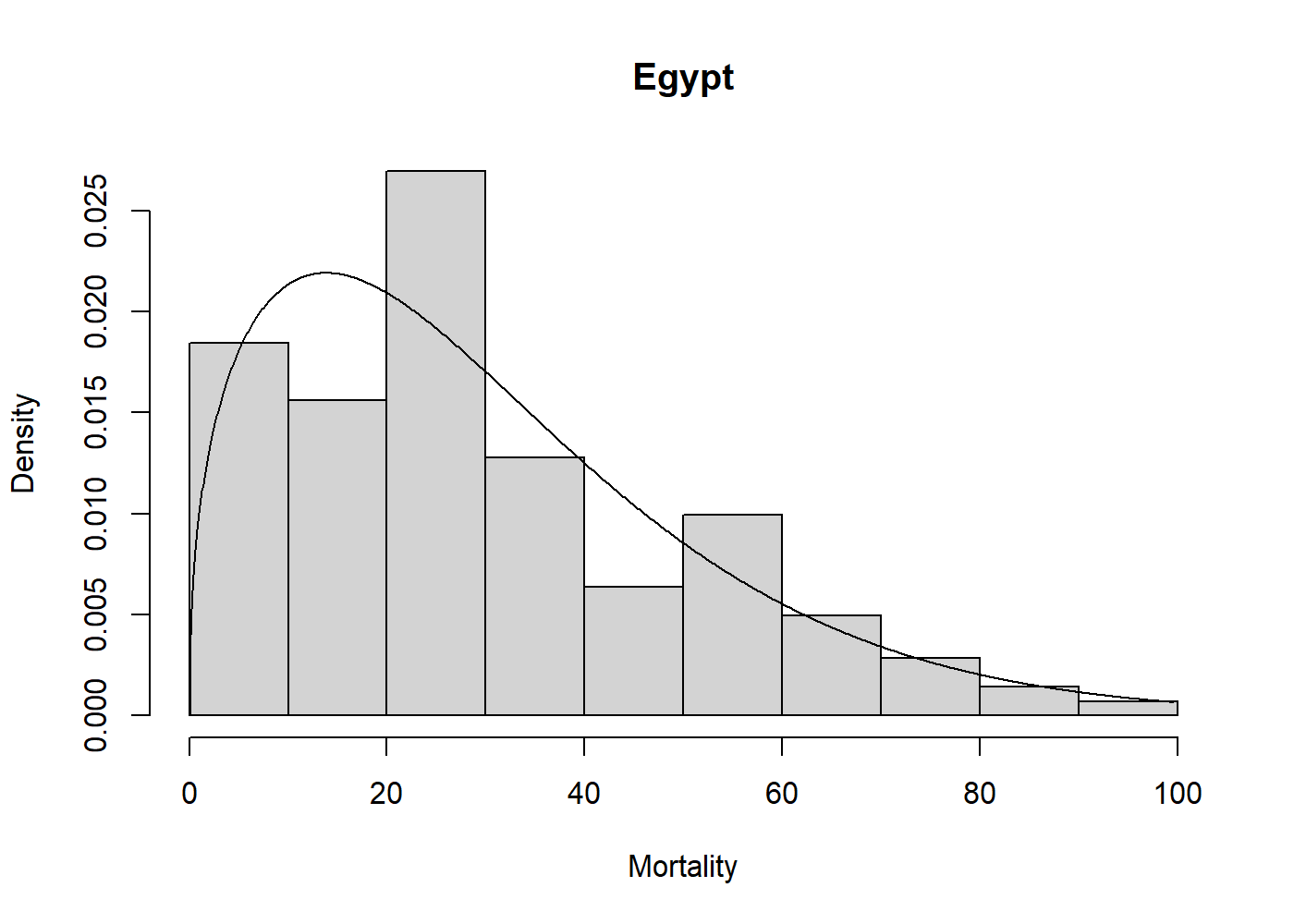

Supported distributions

Continuous distributions

Name univariateML function Package
Cauchy distribution mlcauchy stats
Gumbel distribution mlgumbel extraDistr
Laplace distribution mllaplace extraDistr
Logistic distribution mllogis stats
Normal distribution mlnorm stats
Student t distribution mlstd fGarch
Generalized Error distribution mlged fGarch
Skew Normal distribution mlsnorm fGarch
Skew Student t distribution mlsstd fGarch
Skew Generalized Error distribution mlsged fGarch
Beta prime distribution mlbetapr extraDistr
Exponential distribution mlexp stats
Gamma distribution mlgamma stats
Inverse gamma distribution mlinvgamma extraDistr
Inverse Gaussian distribution mlinvgauss actuar
Inverse Weibull distribution mlinvweibull actuar
Log-logistic distribution mlllogis actuar
Log-normal distribution mllnorm stats
Lomax distribution mllomax extraDistr
Rayleigh distribution mlrayleigh extraDistr
Weibull distribution mlweibull stats
Log-gamma distribution mllgamma actuar
Pareto distribution mlpareto extraDistr
Beta distribution mlbeta stats
Kumaraswamy distribution mlkumar extraDistr
Logit-normal mllogitnorm logitnorm
Uniform distribution mlunif stats
Power distribution mlpower extraDistr
Gompertz distribution mlgompertz extraDistr
Burr distribution mlburr actuar
Inverse Burr distribution mlinvburr actuar
Birnbaum-Saunders mlfatigue extraDistr

Discrete distributions

Name univariateML function Package
Poisson distribution mlpois stats
Negative binomial distribution mlnbinom stats
Binomial distribution mlbinom stats
Geometric distribution mlgeom stats
Zipf distribution mlzipf sads
Zero-inflated Poisson distribution mlzip extraDistr
Discrete uniform distribution mldunif extraDistr
Logarithmic series distribution mldunif extraDistr

Implementations

Analytic formulae for the maximum likelihood estimates are used whenever they exist. Most ml*** functions without analytic solutions have a custom made Newton-Raphson solver. These can be much faster than a naïve solution using nlm or optim. For example, mlbeta has a large speedup over the naïve solution using nlm.

# install.packages("microbenchmark")
set.seed(313)
x <- rbeta(500, 2, 7)

microbenchmark::microbenchmark(
  univariateML = univariateML::mlbeta(x),
  naive = nlm(function(p) -sum(dbeta(x, p[1], p[2], log = TRUE)), p = c(1, 1))
)
#> Unit: microseconds
#>          expr    min      lq     mean median     uq     max neval
#>  univariateML  201.4  244.05  349.978  365.6  422.2   791.9   100
#>         naive 8289.4 8652.60 9170.378 8915.3 9288.0 18723.0   100

The maximum likelihood estimators in this package have all been subject to testing, see the tests folder for details.

Documentation

For an overview of the package and its features see the overview vignette. For an illustration of how this package can make an otherwise long and laborious process much simpler, see the copula vignette.

How to Contribute or Get Help

Please read CONTRIBUTING.md for details about how to contribute or get help.