Robust estimation methods for the mean vector, scatter matrix, and covariance matrix (if it exists) from data (possibly containing NAs) under multivariate heavy-tailed distributions such as angular Gaussian (via Tyler’s method), Cauchy, and Student’s t distributions. Additionally, a factor model structure can be specified for the covariance matrix. The latest revision also includes the multivariate skewed t distribution.
The package can be installed from CRAN or GitHub:
# install stable version from CRAN
install.packages("fitHeavyTail")
# install development version from GitHub
devtools::install_github("convexfi/fitHeavyTail")To get help:
library(fitHeavyTail)
help(package = "fitHeavyTail")
?fit_mvtTo cite fitHeavyTail
in publications:
citation("fitHeavyTail")To illustrate the simple usage of the package fitHeavyTail,
let’s start by generating some multivariate data under a Student’s \(t\) distribution with significant heavy
tails (degrees of freedom \(\nu=4\)):
library(mvtnorm) # package for multivariate t distribution
N <- 10 # number of variables
T <- 80 # number of observations
nu <- 4 # degrees of freedom for heavy tails
set.seed(42)
mu <- rep(0, N)
U <- t(rmvnorm(n = round(0.3*N), sigma = 0.1*diag(N)))
Sigma_cov <- U %*% t(U) + diag(N) # covariance matrix with factor model structure
Sigma_scatter <- (nu-2)/nu * Sigma_cov
X <- rmvt(n = T, delta = mu, sigma = Sigma_scatter, df = nu) # generate dataWe can first estimate the mean vector and covariance matrix via the traditional sample estimates (i.e., sample mean and sample covariance matrix):
mu_sm <- colMeans(X)
Sigma_scm <- cov(X)Then we can compute the robust estimates via the package fitHeavyTail:
library(fitHeavyTail)
fitted <- fit_mvt(X)We can now compute the estimation errors and see the significant improvement:
sum((mu_sm - mu)^2)
#> [1] 0.2857323
sum((fitted$mu - mu)^2)
#> [1] 0.1487845
sum((Sigma_scm - Sigma_cov)^2)
#> [1] 5.861138
sum((fitted$cov - Sigma_cov)^2)
#> [1] 4.663539To get a visual idea of the robustness, we can plot the shapes of the covariance matrices (true and estimated ones) on two dimensions. Observe how the heavy-tailed estimation follows the true one more closely than the sample covariance matrix:
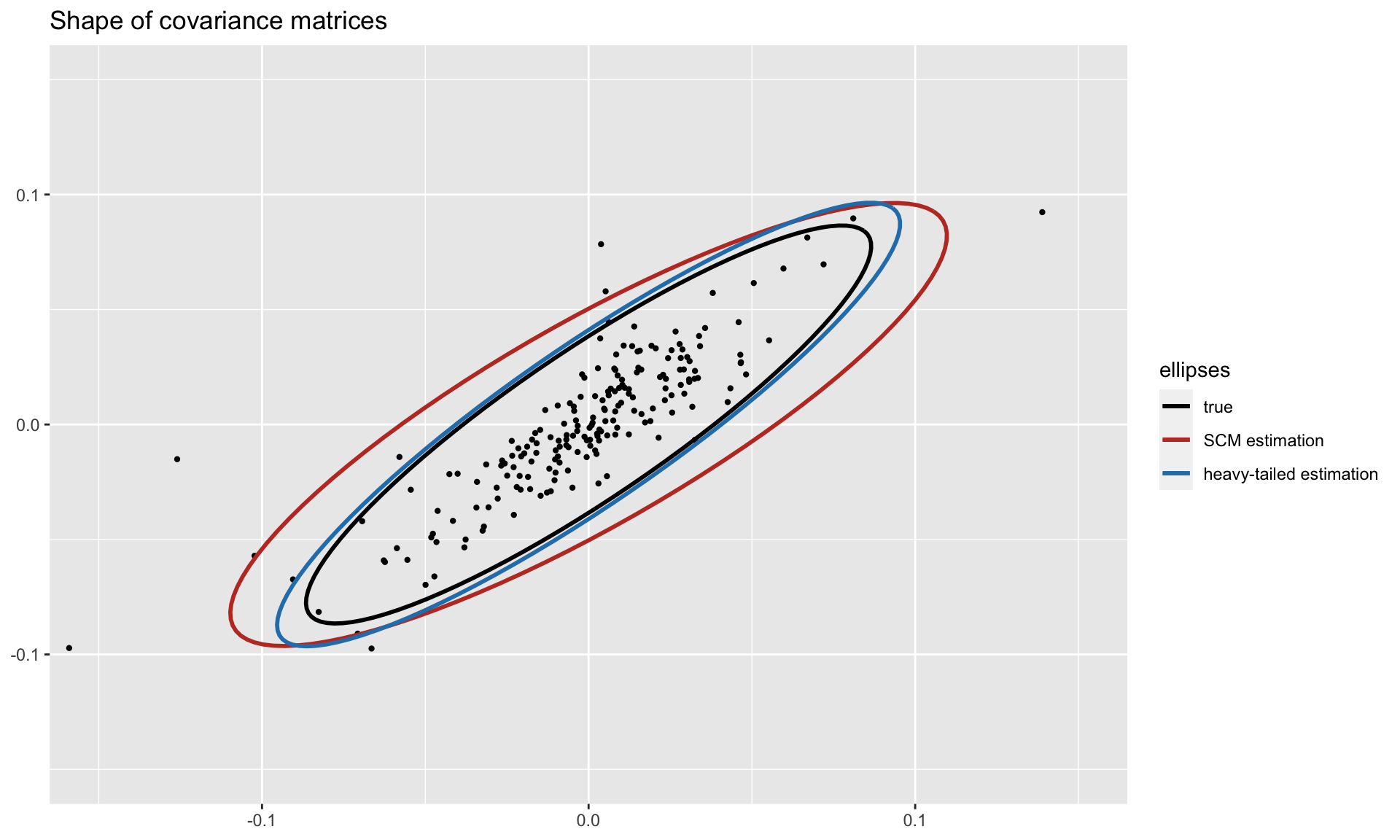
For more detailed information, please check the vignette.
README file: GitHub-readme.
Vignette: CRAN-vignette and GitHub-vignette.