Bayesian Spatial Blind Source Separation via Thresholded Gaussian Process.
Install the released version of BSPBSS from Github with:
devtools::install_github("benwu233/BSPBSS")This is a basic example which shows you how to solve a common problem.
First we load the package and generate simulated images with a probabilistic ICA model:
library(BSPBSS)
set.seed(612)
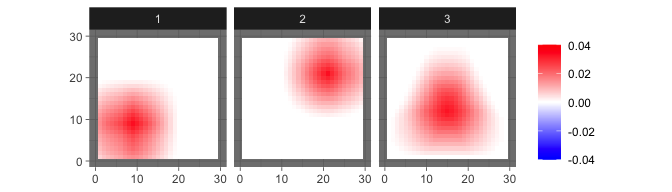
sim = sim_2Dimage(length = 30, sigma = 5e-4, n = 30, smooth = 6)The true source signals are three 2D geometric patterns (set
smooth=0 to generate patterns with sharp edges).
levelplot2D(sim$S,lim = c(-0.04,0.04), sim$coords)
which generate observed images such as
levelplot2D(sim$X[1:3,], lim = c(-0.12,0.12), sim$coords)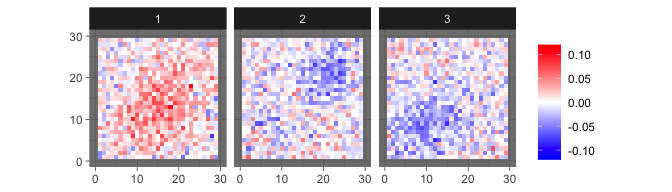
Then we generate initial values for mcmc,
ini = init_bspbss(sim$X, sim$coords, q = 3, ker_par = c(0.1,50), num_eigen = 50)and run!
res = mcmc_bspbss(ini$X,ini$init,ini$prior,ini$kernel,n.iter=2000,n.burn_in=1000,thin=10,show_step=1000)
#> iter 1000 Sat Oct 1 22:12:33 2022
#>
#> stepsize_zeta 0.0167947 accp_rate_zeta 0.34
#> iter 2000 Sat Oct 1 22:12:36 2022
#>
#> stepsize_zeta 0.0167947 accp_rate_zeta 0.37Then the results can be summarized by
res_sum = sum_mcmc_bspbss(res, ini$X, ini$kernel, start = 101, end = 200, select_p = 0.5)and shown by
levelplot2D(res_sum$S, lim = c(-1.3,1.3), sim$coords)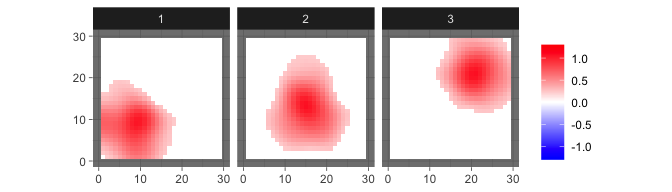
For comparison, we show the estimated sources provided by informax ICA here.
levelplot2D(ini$init$ICA_S, lim = c(-1.7,1.7), sim$coords)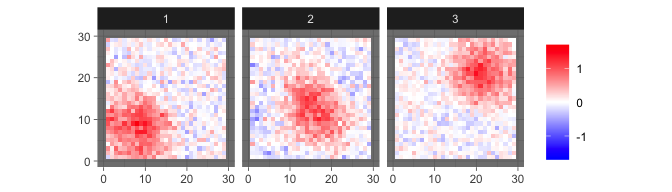
We may overspecify the number of components and still obtain reasonable results.
ini = init_bspbss(sim$X, sim$coords, q = 5, ker_par = c(0.1,50), num_eigen = 50)
res = mcmc_bspbss(ini$X,ini$init,ini$prior,ini$kernel, n.iter=2000,n.burn_in=1000,thin=10,show_step=1000)
#> iter 1000 Sat Oct 1 22:12:40 2022
#>
#> stepsize_zeta 0.0104649 accp_rate_zeta 0.35
#> iter 2000 Sat Oct 1 22:12:43 2022
#>
#> stepsize_zeta 0.0104649 accp_rate_zeta 0.43
res_sum = sum_mcmc_bspbss(res, ini$X, ini$kernel, start = 101, end = 200, select_p = 0.5)
levelplot2D(res_sum$S, lim = c(-1.3,1.3), sim$coords)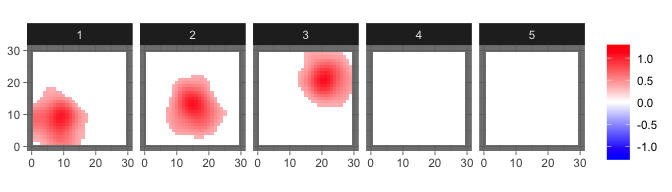
Install a small pack contains simulated NIfTI images and MNI152 template.
devtools::install_github("benwu233/SIMDATA")Load and take a glance at the data.
data_path = system.file("extdata",package="SIMDATA")
t1_3mm = neurobase::readNIfTI2(paste0(data_path,"/template/MNI152_T1_3mm.nii.gz"))
sim_4d = neurobase::readNIfTI2(paste0(data_path,"/sim_4d/sim_4d.nii.gz"))
mask = neurobase::readNIfTI2(paste0(data_path,"/sim_4d/mask.nii.gz"))
neurobase::ortho2(t1_3mm, y=sim_4d[,,,1])
Conduct BSPBSS.
X = pre_nii(sim_4d,mask)
ini = init_bspbss(X$data, X$coords, dens = 0.5, q = 3, ker_par = c(0.01, 120), num_eigen = 200)
res = mcmc_bspbss(ini$X,ini$init,ini$prior,ini$kernel,n.iter=3000,n.burn_in=2000,thin=10,show_step=1000,subsample_p=0.005)
#> iter 1000 Sat Oct 1 22:14:38 2022
#>
#> stepsize_zeta 0.00296575 accp_rate_zeta 0.42
#> iter 2000 Sat Oct 1 22:16:28 2022
#>
#> stepsize_zeta 0.00769239 accp_rate_zeta 0.42
#> iter 3000 Sat Oct 1 22:18:19 2022
#>
#> stepsize_zeta 0.00769239 accp_rate_zeta 0.41
res_sum = sum_mcmc_bspbss(res, ini$X, ini$kernel, start = 201, end = 300, select_p = 0.5)Output:
ICs = output_nii(res_sum$S,sim_4d,X$coords,file=NULL,std=TRUE)Component 1:
neurobase::ortho2(t1_3mm,y=ICs[,,,1]) Component 2:
Component 2:
neurobase::ortho2(t1_3mm,y=ICs[,,,2]) Component 3:
Component 3:
neurobase::ortho2(t1_3mm,y=ICs[,,,3])